Back in June, I attended DDD Europe 2023.
It was the first time I was at this conference, but I liked it a lot, and I was
intrigued by
Jérémie Chassaing's talk,
in which he used a decider to keep track of the internal state
of aggregates.
I don't know a lot (yet?) about functional programming, but I was charmed
by this elegant way to work with commands and events. So I
wanted to experiment with deciders as well.
As it turns out, I have an ideal project for doing this kind of
experiments:
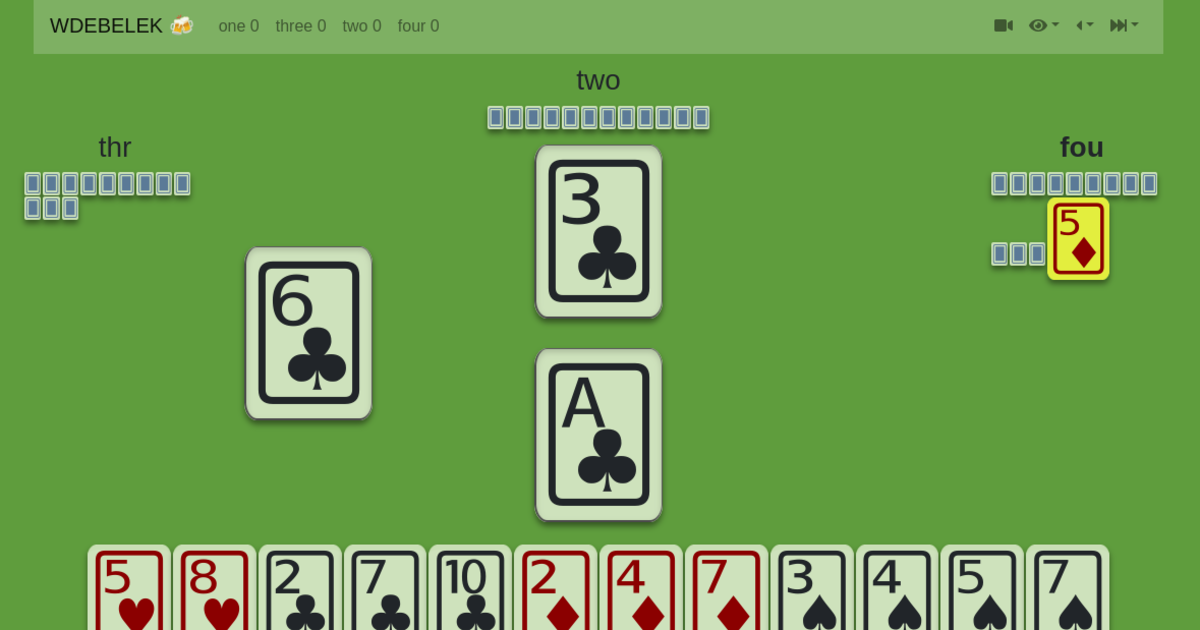
dikdikdik, my web based
score sheet for the wiezen (whist) card
game. It already had commands and events, so using a decider should not
be too hard.

Dikdikdik has two aggregates: a table (as in a piece of furniture, the
table is where the players sit down, and play their games)
and a score sheet. Initially those aggregates had methods that emitted
events, and other methods that applied those events to their internal
states. The latter ones were also used to rebuild the aggregates based
on their event streams, since dikdikdik is also an event sourced application.
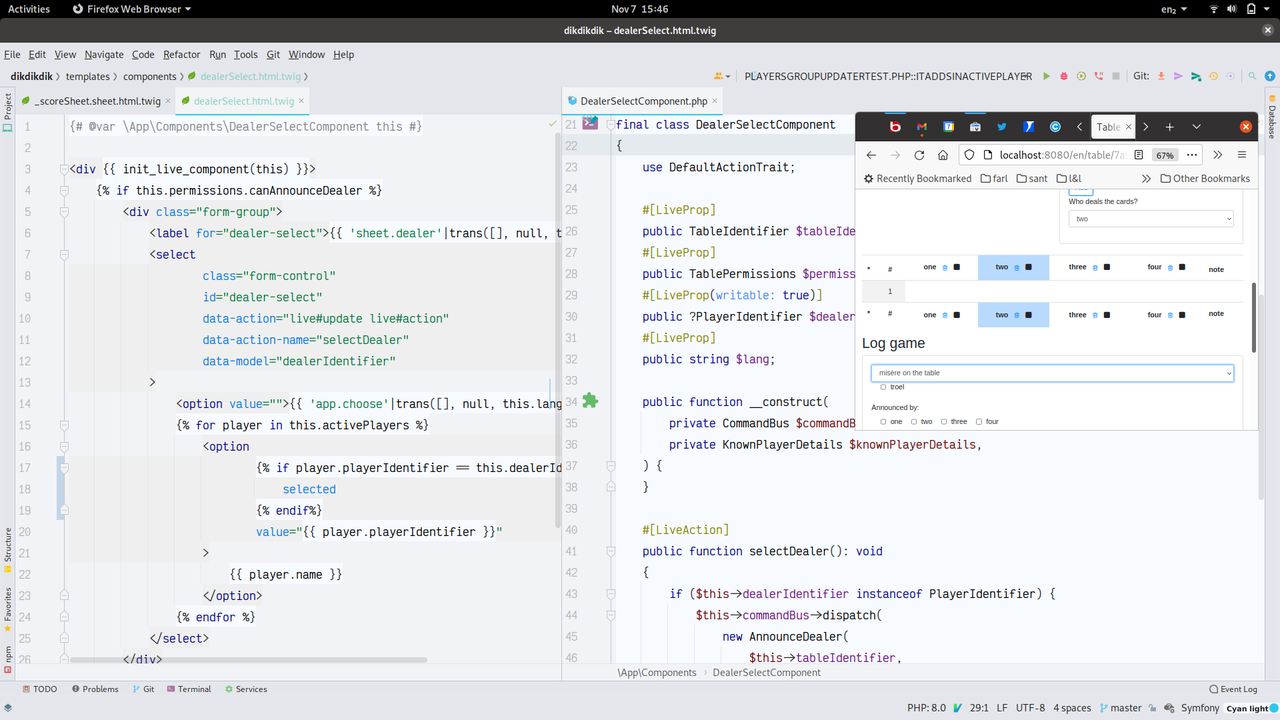
In a first step, I replaced the table entity by a TableDecider and a
TableInternalState class. The idea is that when you pass
the internal state of a table and a command to the
decide-method of the
TableDecider,
it produces events, describing
what happens. When passing those events with the internal state to
the evolve-method of the decider, it
applies the events, creating an updated internal state.
I could use this decider pattern to implement event sourcing, and it also
allowed me to create a kind of testing
framework, that made it easy to create given-when-then-unit tests in a quite elegant
way, see e.g.
this test that tests joining players.
I created the decider in a more-or-less test driven way, by converting my old
tests for the Table aggregate to new tests for the table decider, and then make them
pass by converting the old logic to the decider based logic.
This conversion was interesting, because it made me look back into
the existing code for the write side of the table. And whenever I see
code I wrote a couple of months or years ago, I am reminded about the
things I learned since then. That's a good thing, I presume. Other pieces
of the code have become less relevant, since the project has changed as well
during the last couples of years. I created a couple of issues on gitlab
for the oddities I enountered,
e.g. #304,
#308,
#302.
When all unit tests passed, it didn't take a lot of work to make the integration tests
and e2e tests to be all green as well. Which made me happy, because I think this
was an indication that the
degree of decoupling in my project is low.
If you look at the merge request
(which I reviewed en merged myself, since I am the only developer on the project 😉),
you will notice that almost all changes are in the Domain\WriteModel\Table namespace,
and almost no other things needed to change. The other aggregate, the
ScoreSheet, still uses my old way of working, and guess what: that doesn't matter.
The score sheet doesn't need to care about the internal workings of the table,
and vice versa, the events are the only things that pass the boundries between them.
All with all, there were two other things I needed to change. One thing, was the
validation of the games that can be logged. Now I can use a service for this, that I
can nicely inject into the decider, which is way more elegant than what I did before to
let the aggregate class validate the logged games. (The validation service still has some
issues in its current form, but it is already injected; that's something.)
Another thing is that the decider is aware of the initial state of the aggregate.
Previously, I prepared the initial state by handling the event TableCleared. Now
this event is not really needed anymore, but in my integration tests I still
(ab)use it to reset the read models.
Another interesting change that happened, when introducing the decider, is that I don't
have a dedicated handler for each command anymore. Which feels a little strange to me, I
always learnt that each command should have its own handler.
Now the TableDecider takes every TableCommand, and calls
the handler function that corresponds to the command.
But I guess these functions are the handlers now, which may be fine.
Anyway, I am happy about the result I've got so far. I think I will already
release this to score.rijkvanafdronk.be at the
end of this month, so that we can try it out during the next meetup of our
wiezen club. (Of course everything should just work,
since all tests are green,
but I want to use the application quickly after the release, so that we would
notice any bugs that are not covered by the tests.)
So what's next:
Now that the write side for the table is handled by a decider, I will also replace
the one for the score sheet. Since the ScoreSheet class is much smaller than
the Table class was, this should take less time than converting the table, but
I also have little free time to develop these days, so we will see how this turns out.
And then there's the process manager, that passes commands to the score sheet when games
are played at the table. I think Jérémy did something like this in his talk, by
combining deciders, but I will probably have to watch a recording of his talk again,
because I'm not sure anymore about how this works.
Another thing I want to do, is add the generic decider classes I created to the
krakboem libray I created for my own
event sourced projecs. That library needs some updates as well, because it was
created when php 7.4 was a thing.
For a short period of time, I had timelines for the new features of dikdikdik.
But not anymore, because life happens, and I will see when I have time to code.
Anyway, I want to thank
Jérémie for his inspiring talk. I'm
glad I got this far already, and we'll see what the future brings.
Until then:
have a nice time playing whist.